准确率，精确率，召回率和AUC曲线，PR曲线

发布： 2019-08-17 分类： Machine Learning 评论：阅读：

我们都知道机器学习要建模，但是对于模型性能的好坏（即模型的泛化能力），我们并不知道是怎样的，很可能这个模型就是一个差的模型，泛化能力弱，对测试集不能很好的预测或分类。那么如何知道这个模型是好是坏呢？我们必须有个评判的标准。为了了解模型的泛化能力，我们需要用某个指标来衡量，这就是性能度量的意义。有了一个指标，我们就可以对比不同模型了，从而知道哪个模型相对好，那个模型相对差，并通过这个指标来进一步调参逐步优化我们的模型。

混淆矩阵（TP TN FP FN）

True Positives,TP：预测为正样本，实际也为正样本的特征数
False Positives,FP：预测为正样本，实际为负样本的特征数
True Negatives,TN：预测为负样本，实际也为负样本的特征数
False Negatives,FN：预测为负样本，实际为正样本的特征数

True / False：是针对原样本而言的。
Positive / Negative：是针对预测结果而言的。

准确率 (accuracy)

既然是个分类指标，我们可以很自然的想到准确率，准确率的定义是预测正确的结果占总样本的百分比，其公式如下：

$$accuracy = \frac{TP+TN}{TP+TN+FP+FN}$$

虽然准确率可以判断总的正确率，但是在样本不平衡的情况下，并不能作为很好的指标来衡量结果。举个简单的例子，比如在一个总样本中，正样本占90%，负样本占10%，样本是严重不平衡的。对于这种情况，我们只需要将全部样本预测为正样本即可得到90%的高准确率，但实际上我们并没有很用心的分类，只是随便无脑一分而已。这就说明了：由于样本不平衡的问题，导致了得到的高准确率结果含有很大的水分。即如果样本不平衡，准确率就会失效。

正因为如此，也就衍生出了其它两种指标：精准率和召回率。

精确率 (precision)

精确率：预测为正的样本中有多少是真的正样本。精确率和准确率看上去有些类似，但是完全不同的两个概念。精准率代表对正样本结果中的预测准确程度，而准确率则代表整体的预测准确程度，既包括正样本，也包括负样本。

$$precision = \frac{TP}{TP+FP}$$

召回率 (recall)

召回率，又叫查全率，它是针对原样本而言的，它的含义是样本中为正的，有多少被预测为正。

$$recall = \frac{TP}{TP+FN}$$

召回率的应用场景：比如拿网贷违约率为例，相对好用户，我们更关心坏用户，不能错放过任何一个坏用户。因为如果我们过多的将坏用户当成好用户，这样后续可能发生的违约金额会远超过好用户偿还的借贷利息金额，造成严重偿失。召回率越高，代表实际坏用户被预测出来的概率越高，它的含义类似：宁可错杀一千，绝不放过一个。

特异度 (specificity)

特异度被定义为：样本中为负的，有多少被预测为负。和召回率刚好相反，一个针对正样本而言，一个针对负样本而言。

$$specificity = \frac{TN}{TN+FP}$$

F_1值

F1值 = 精确率 * 召回率 * 2 / (精确率 + 召回率) （F1值即为精确率和召回率的调和平均值）

$$F_1 = \frac{P * R * 2}{P + R}$$

不妨举这样一个例子：某池塘有1400条鲤鱼，300只虾，300只鳖。现在以捕鲤鱼为目的。撒一大网，逮着了700条鲤鱼，200只虾，100只鳖。那么，这些指标分别如下：

1
2
3

P (precision) = 700 / (700 + 200 + 100) = 70%
R (recall) = 700 / 1400 = 50%
F1 = 70% * 50% * 2 / (70% + 50%) = 58.3%

不妨看看如果把池子里的所有的鲤鱼、虾和鳖都一网打尽，这些指标又有何变化：

1
2
3

P (precision) = 1400 / (1400 + 300 + 300) = 70%
R (recall) = 1400 / 1400 = 100%
F1 = 70% * 100% * 2 / (70% + 100%) = 82.35%

由此可见，精确率是评估捕获的成果中目标成果所占得比例；召回率，顾名思义，就是从关注领域中，召回目标类别的比例；而F值，则是综合这二者指标的评估指标，用于综合反映整体的指标。

当然希望检索结果precision越高越好，同时recall也越高越好，但事实上这两者在某些情况下有矛盾的。比如极端情况下，我们只搜索出了一个结果，且是准确的，那么precision就是100%，但是recall就很低；而如果我们把所有结果都返回，那么recall是100%，但是precision就会很低。因此在不同的场合中需要自己判断希望precision比较高或是recall比较高。如果是做实验研究，可以绘制Precision-Recall曲线来帮助分析。

有时候我们对精确率和召回率并不是一视同仁，比如有时候我们更加重视精确率。我们用一个参数 $\beta$ 来度量两者之间的关系。如果 $\beta>1$, 召回率有更大影响，如果 $\beta<1$, 精确率有更大影响。自然，当 $\beta=1$ 的时候，精确率和召回率影响力相同，和F1形式一样。含有度量参数 $\beta$ 的F1我们记为 $F_\beta$, 严格的数学定义如下：

$$𝐹_𝛽=\frac{(1+𝛽^2)∗𝑃∗𝑅}{𝛽^2∗𝑃+𝑅} $$

RoC 曲线与 AUC 值

🎋. 灵敏度 TPR (true positive rate) (同召回率)：真实样本中为正的，有多少被预测为正

🎋. 1-特异度：FPR (false positive rate)：真实样本为负的，有多少被预测为正

$$FPR = \frac{FP}{FP+TN}$$

🎋. ROC曲线与AUC值：以TPR为y轴，以FPR为x轴，我们就直接得到了RoC曲线。从FPR和TPR的定义可以理解，TPR越高，FPR越小，我们的模型和算法就越高效。也就是画出来的RoC曲线越靠近左上越好。如下图左图所示。从几何的角度讲，RoC曲线下方的面积越大越大，则模型越优。所以有时候我们用RoC曲线下的面积，即AUC（Area Under Curve）值来作为算法和模型好坏的标准。

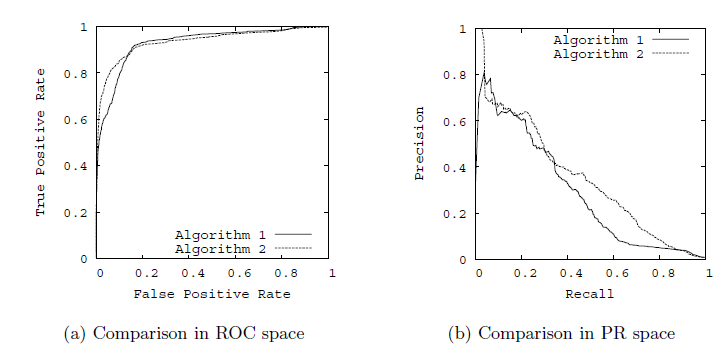
🎋. PR曲线：以精确率为y轴，以召回率为x轴，我们就得到了PR曲线。仍然从精确率和召回率的定义可以理解，精确率越高，召回率越高，我们的模型和算法就越高效。也就是画出来的PR曲线越靠近右上越好。如上图右图所示。

参考链接：https://segmentfault.com/a/1190000016686335
参考链接：https://www.cnblogs.com/pinard/p/5993450.html

混淆矩阵 （TP TN FP FN）