字符串匹配算法－KMP算法

发布： 分类： 评论： 阅读：

给定一个主串S及一个模式串P，判断模式串是否为主串的子串；若是，返回匹配的第一个元素的位置，否则返回-1；

如S=“abcd”，P=“bcd”，则返回1；S=“abcd”，P=“acb”，返回-1。

朴素算法：回溯法

最简单的方法就是遍历主串S和模式串P，逐个字符进行匹配，不匹配时返回开始的位置，从主串S的下一个字符开始，继续域模式串P匹配。以一张动图来说明：

img

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
//查找出模式串patn在主串src中第一次出现的位置
//返回patn在src中出现的位置，当src中并没有patn时，返回-1
int search(String src, String patn) {
    int i=0, j=0;
    while(i<src.length() && j<patn.length()) {
        if(src.charAt(i)==patn.charAt(j)) {
            i += 1;
            j += 1;
        }
        else {
            //否则，指针回溯，重新开始匹配
            i = i - j + 1;  //退回到最开始时比较的位置+1
            j = 0;
        }
    }
    if( j >= patn.length() )
        return i - plen;  //如果字符串相同的长度大于模式串的长度，则匹配成功
    else
        return -1;
}

朴素算法理解简单，但两个串都有依次遍历，时间复杂度为O(n*m)，效率不高。

优化算法：KMP算法

KMP算法的核心，是一个被称为部分匹配表 (Partial Match Table) 的数组。

PMT表：对于模式字符串“abababca”，它的PMT如下表所示：

img

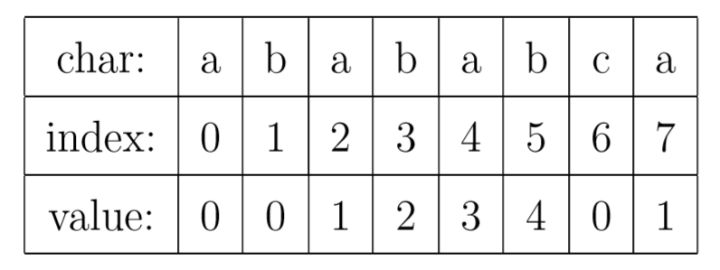
第一行：字符串的每个字符；
第二行：每个字符的索引；
重要的是value值：PMT中的value是字符串的前缀集合与后缀集合的交集中最长元素的长度。

例如，对于 “aba” ，它的前缀集合为{“a”, “ab”}，后缀集合为{“ba”, “a”}。两个集合的交集为{“a”}，那么长度最长的元素就是字符串 “a” 了，长度为1，所以对于 “aba” 而言，它在PMT表中对应的值就是1。再比如，对于字符串 “ababa”，它的前缀集合为{“a”, “ab”, “aba”, “abab”}，它的后缀集合为{“baba”, “aba”, “ba”, “a”}， 两个集合的交集为{“a”, “aba”}，其中最长的元素为 “aba”，长度为3，则 “ababa” 在PMT表中对应的值就是3。

如何使用PMT表加速字符串的查找：

  • 主字符串为：“ababababca” -> main_string[0:len_m]
  • 模式字符串为：“abababca” -> pattern_string[0:len_p]

在主字符串 main_string 中查找模式字符串 pattern_string。当 main_string[i] != pattern_string[j] 时，我们知道，main_string[i-j:i-1] 和 pattern_string[0:j-1] 是完全一致的。

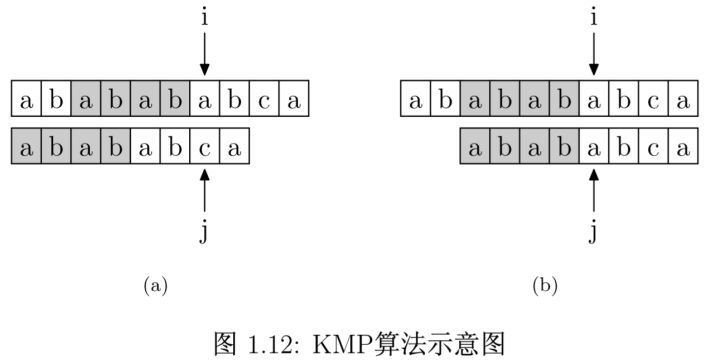
具体到下图：i=j=6 时，两个字符不相等，main_string[0:5] = pattern_string[0:5] = “ababab”

那么此时我们应该如何操作：从PMT表中，我们能够看到 PMT[5] 的值（ pattern_string[0:5] 中的前缀集合与后缀集合的交集中最长元素的长度）， PMT[5]=4，也就是说，该字符串中，前缀和后缀相同的最长长度为4，也就是说，pattern_string[0:5] 前四位和后四位是相同的。因为 main_string[0:5] = pattern_string[0:5] ,也就是说，pattern_string[0:5] 的前四位和 main_string[0:5] 的后四位是相同的，那么我们就可以直接进行移动了，保持 i 指针不动，然后将 j 指针指向模式字符串的 PMT[5] 位即可。

简言之，以图中的例子来说，在 i 处失配，那么主字符串和模式字符串的前边6位就是相同的。又因为模式字符串的前6位，它的前4位前缀和后4位后缀是相同的，所以我们推知主字符串 i 之前的4位和模式字符串开头的4位是相同的。就是图中的灰色部分。那这部分就不用再比较了。

img

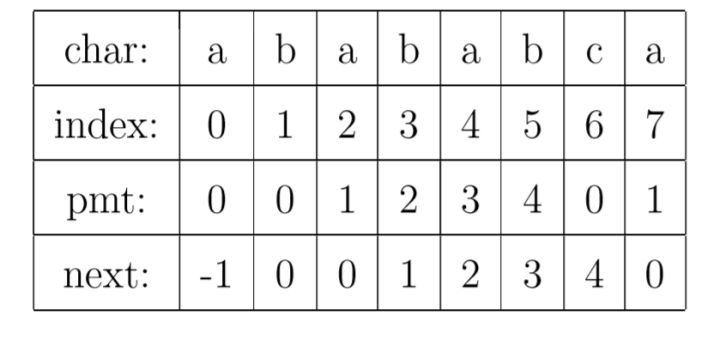
有了上面的思路，我们就可以使用PMT加速字符串的查找了。我们看到如果是在 j 位失配，那么影响 j 指针回溯的位置的其实是第 j −1 位的 PMT 值，所以为了编程的方便， 我们不直接使用PMT数组，而是将PMT数组向后偏移一位。我们把新得到的这个数组称为next数组。下面给出根据next数组进行字符串匹配加速的字符串匹配程序。其中要注意的一个技巧是，在把PMT进行向右偏移时，第0位的值，我们将其设成了-1，这只是为了编程的方便，并没有其他的意义。在本节的例子中，next数组如下表所示。

img

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int KMP(String text, String pattern) {
    int i = 0, j = 0;
    while (i < text.length() && j < pattern.length()) {
        if (j == -1 || text.charAt(i)==pattern.charAt(j)) {
            i++;
            j++;
        }
        else 
           j = next[j];
        if (j == pattern.length())
           return i - j;  // 返回text中的开始位置
        else 
           return -1;     // 匹配失败
    }
}

如何快速求next数组

其实，求next数组的过程完全可以看成字符串匹配的过程，即以模式字符串为主字符串，以模式字符串的前缀为目标字符串，一旦字符串匹配成功，那么当前的next值就是匹配成功的字符串的长度。

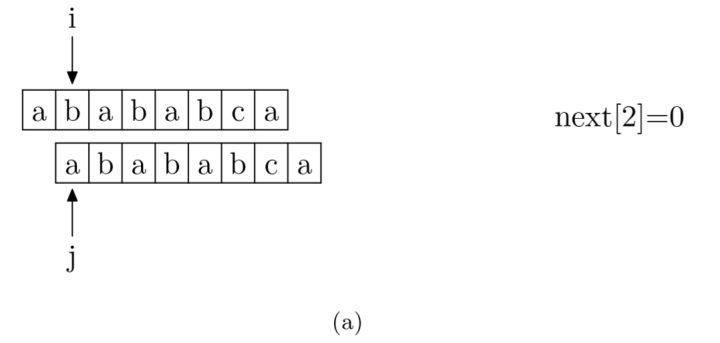
具体来说，就是从模式字符串的第一位(注意，不包括第0位)开始对自身进行匹配运算。 在任一位置，能匹配的最长长度就是当前位置的next值。如下图所示。

p串错开一位匹配，0起始的p串与1起始的p串，前者是瞄准了p的前缀，后者抛弃了p[0]所以是瞄准p的后缀，双方的公共部分即是公共前后缀。

img

img

img

img

img

1
2
3
4
5
6
7
8
9
10
11
12
13
14
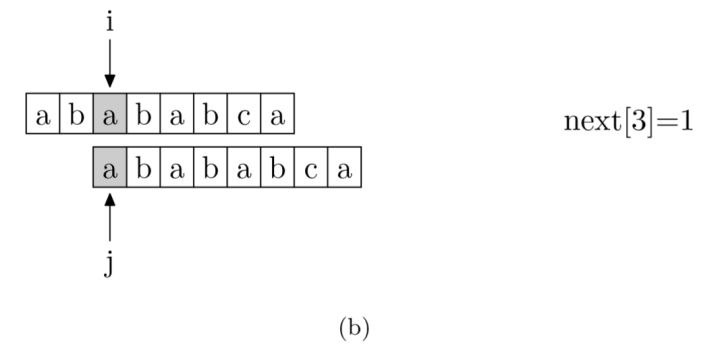
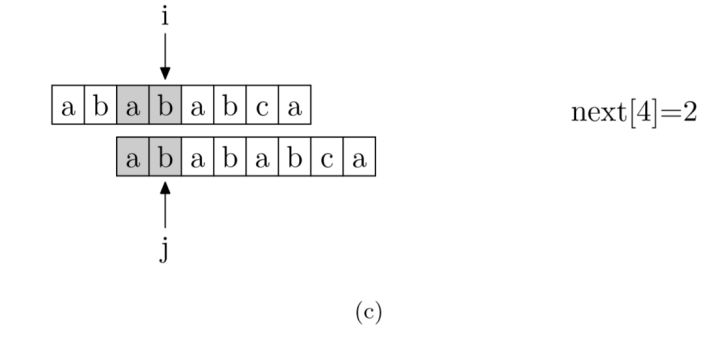
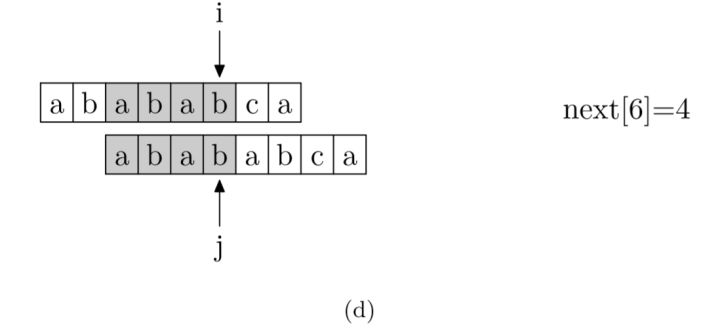
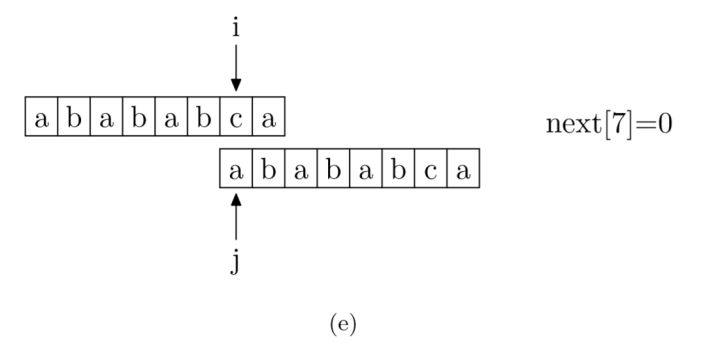
void getNext(String pattern, int[] next) {
    next[0] = -1;
    int i = 0, j = -1;

    while (i < pattern.length()) {
        if (j == -1 || p.charAt(i)==p.charAt(j)) {
            ++i;
            ++j;
            next[i] = j;
        }	
        else
            j = 0;   //next[j];
    }
}
  1. 匹配失败时，总是能够让 pattern 回退到某个位置，使 text 不用回退。
  2. 在字符串比较时，pattern 提供的信息越多，计算复杂度越低。（有兴趣的可以了解一下 Trie 树，这是 text 提供的信息越多，计算复杂度越低的一个例子。）

参考链接：https://www.zhihu.com/question/21923021
参考链接：https://blog.csdn.net/qq_37969433/article/details/82947411