排序算法
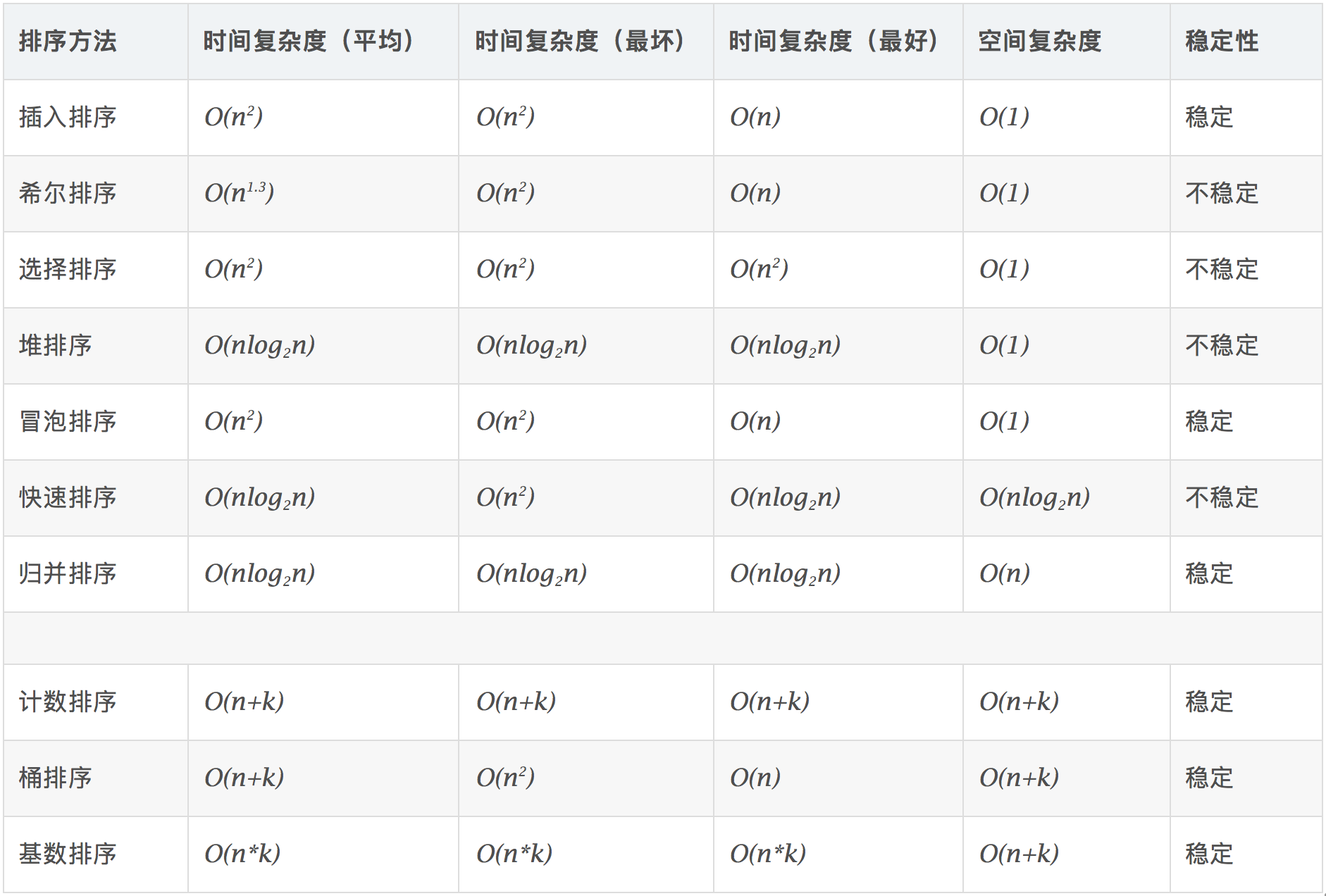
各种排序算法复杂度分析
- 稳定:如果a原本在b前面,而a=b,排序之后a仍然在b的前面。
- 不稳定:如果a原本在b的前面,而a=b,排序之后 a 可能会出现在 b 的后面。
在写排序算法之前,先把每种排序算法都用到的数组元素交换的代码写出来:
1 | public void swap(int[] arr, int i, int j) { |
选择排序 (selection sort)
- 选择出数组中的最小元素,将它与数组的第一个元素进行交换;
- 从剩下的元素中选择出最小的元素,将它与数组的第二个元素进行交换;
- 直到将整个数组排序。
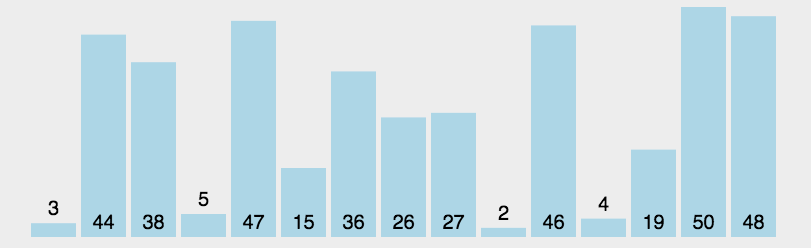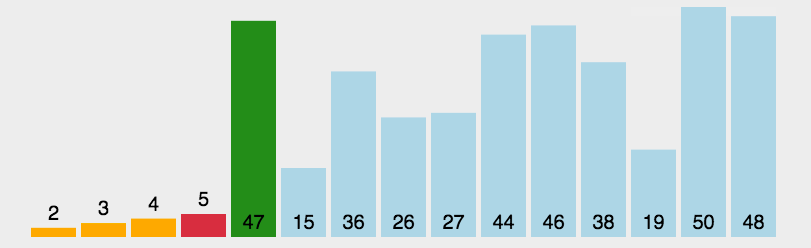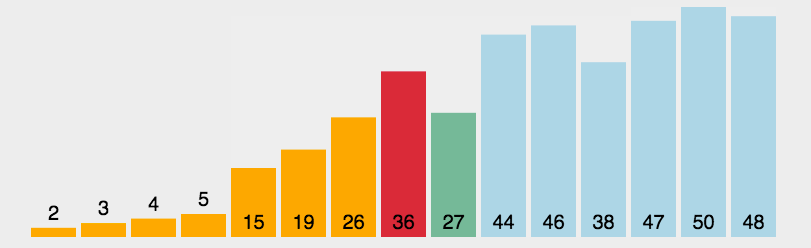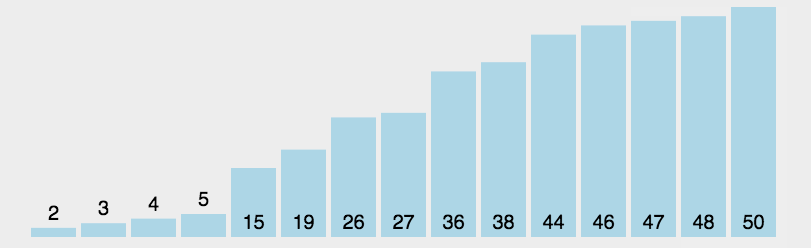
1 | public void selection_sort(int[] arr) { |
算法分析:最稳定的算法之一;时间复杂度为$O(n^2)$;数据规模越小越好;不占用额外空间。
插入排序 (insert sort)
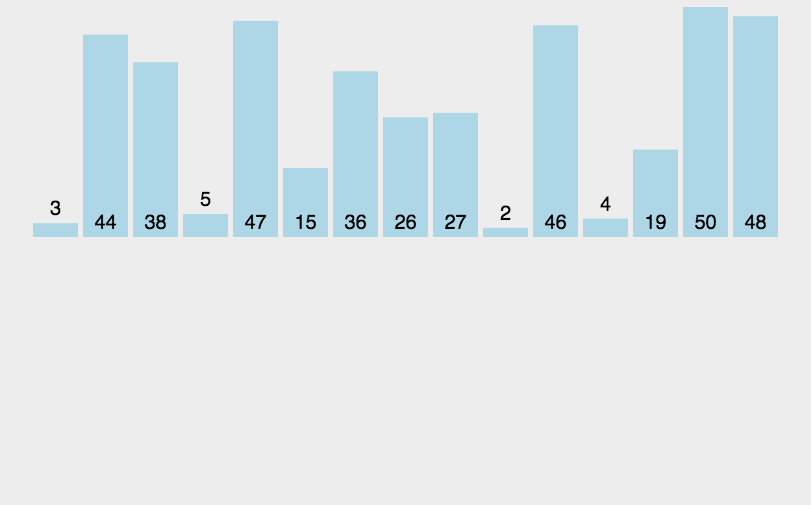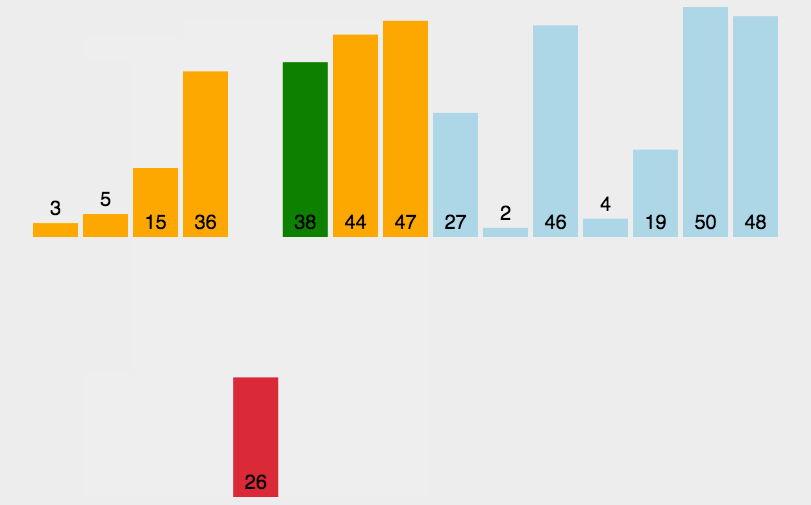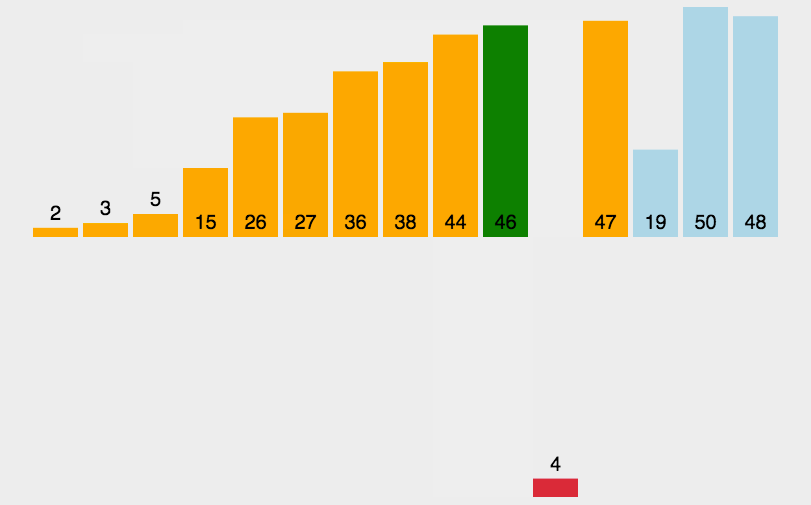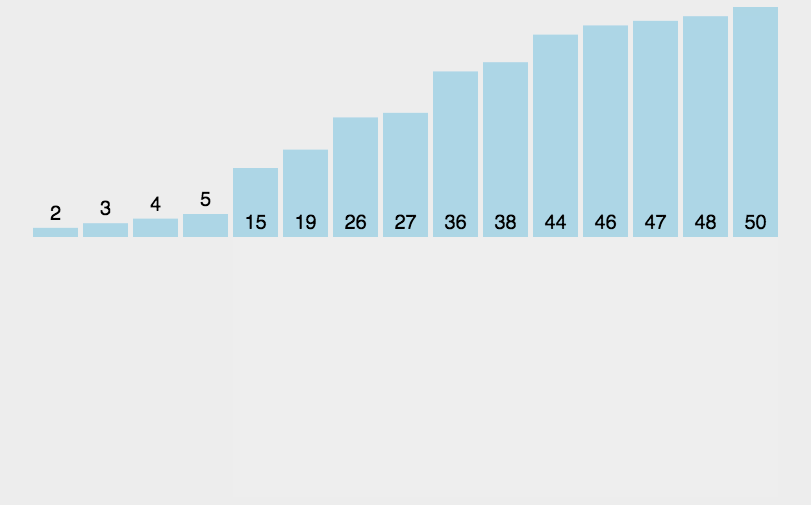
- 从左到右,每次将当前元素插入到左侧已经排好序的数组当中,使插入后左部分数组依然有序;
- 第 j 个元素不断与左侧元素进行比较,arr[j] < arr[j-1] 就交换两个元素的位置,并j=j-1。
1 | public void insert_sort(int[] arr) { |
上面的代码每次都要交换位置,会浪费时间,优化代码:
1 | for(int i=0;i<arr.length;i++) { |
算法分析:插入排序通常采用in-place排序(即只需要用O(1)的额外空间的排序),所以在排序过程中,需要不断把元素进行后移,为新的元素插入提供空间。
冒泡排序 (bubble sort)
- 将当前元素与后面的元素逐个比较,若a[j] > a[j+1],就进行交换,每轮排序后最大值会排到后面去;
- 当执行一轮循环后,没有发生交换,则表示数组已经有序。
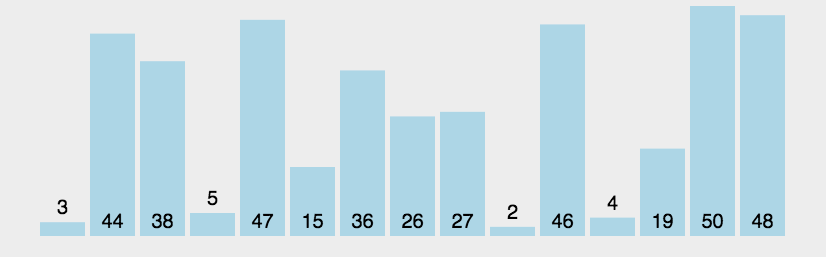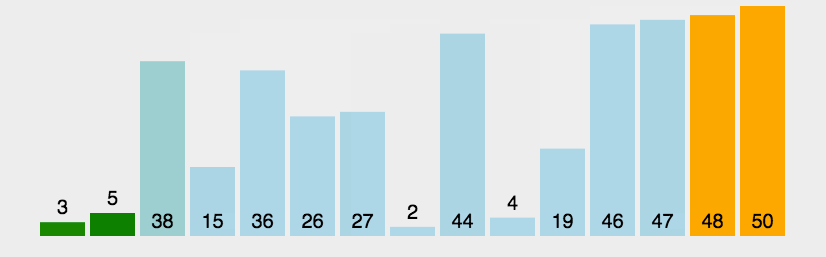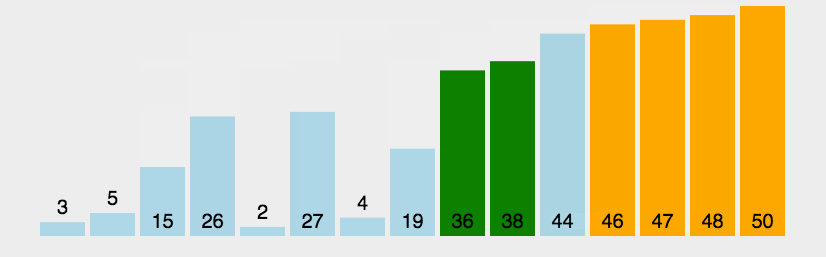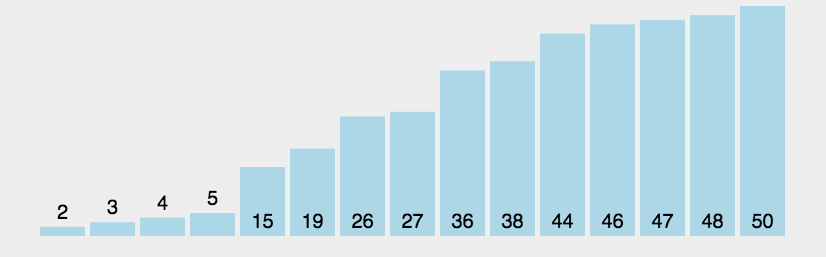
1 | public void bubble_sort(int[] arr) { |
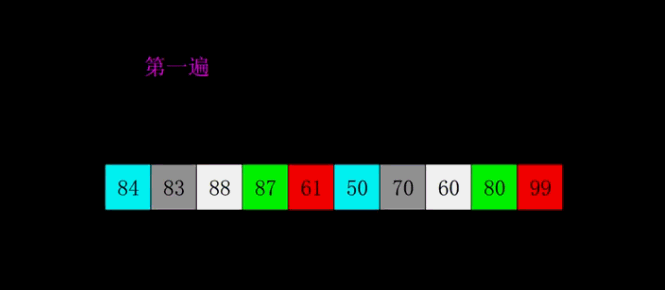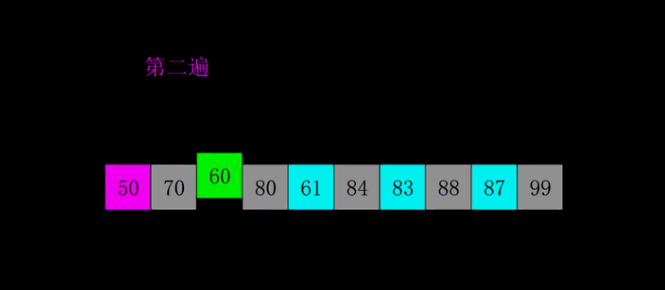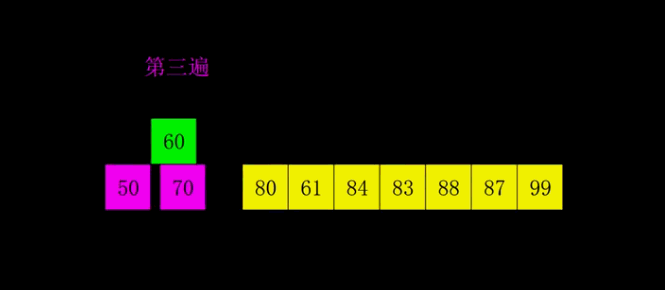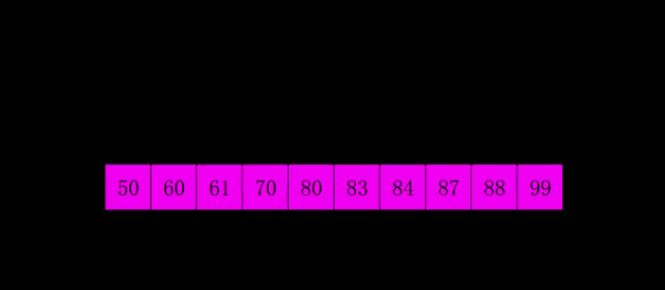
希尔排序 (shell sort)
- 希尔排序会优先比较距离较远的元素。又叫缩小增量排序。
- 希尔排序把记录按下标的一定增量分组,对每组使用直接插入排序算法排序;
- 随着增量逐渐减少,每组包含的元素越来越多,当增量减至1时,整个数组恰被分成一组,算法便终止。
1 | public static void shell_sort(int[] arr){ |
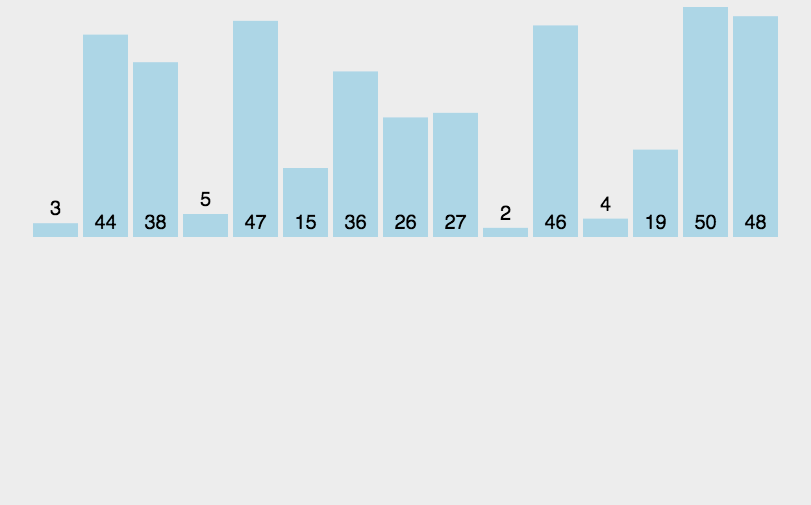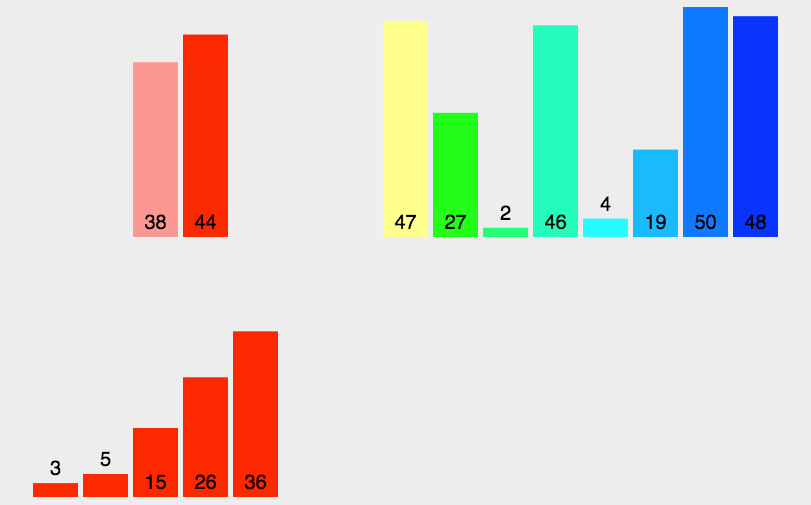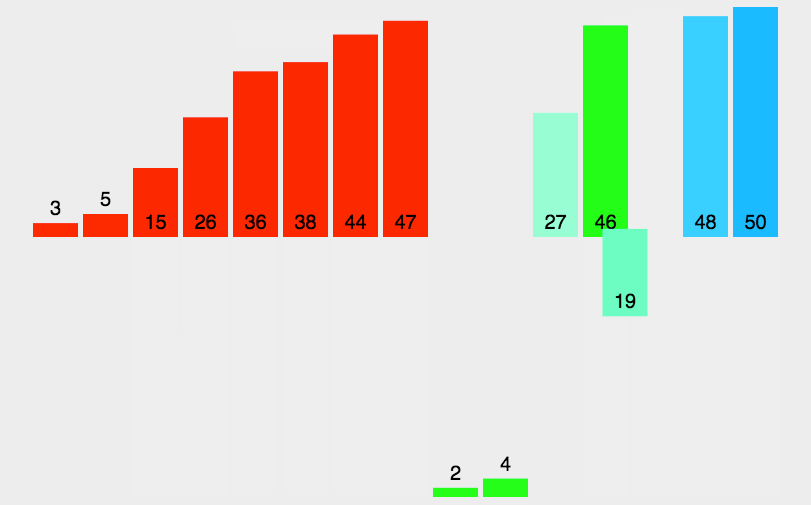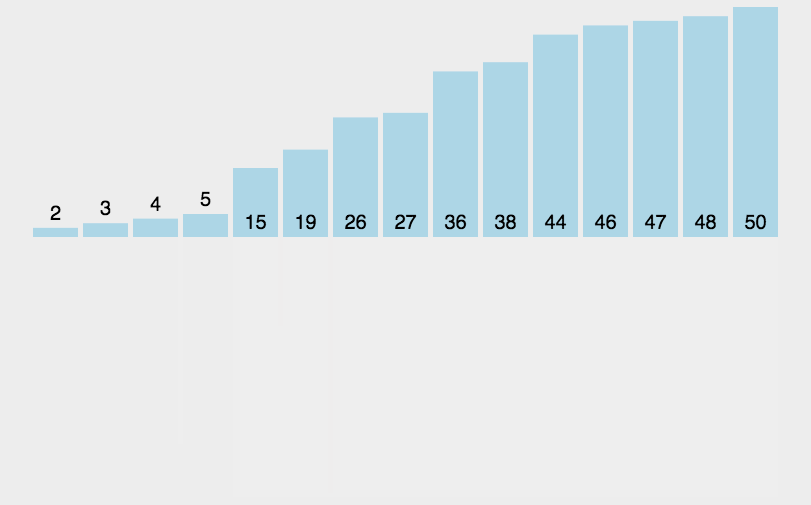
归并排序 (merge sort)
- 归并排序采用了分治的思想,将大数组化为一个个的小数组去处理,然后再归并到一起。
1 | public static void merge_sort(int[] arr,int left, int right) { |
快速排序 (quick sort)
1 | 一趟快速排序的算法是: |
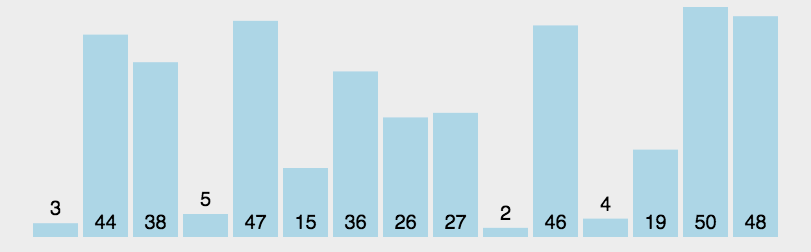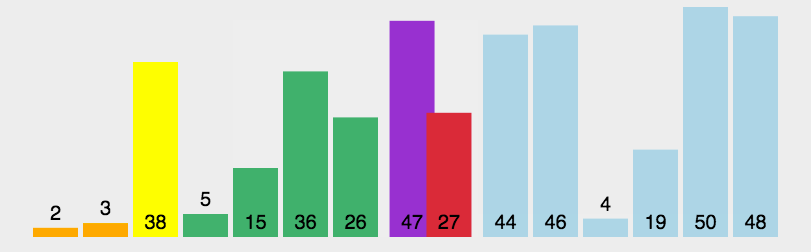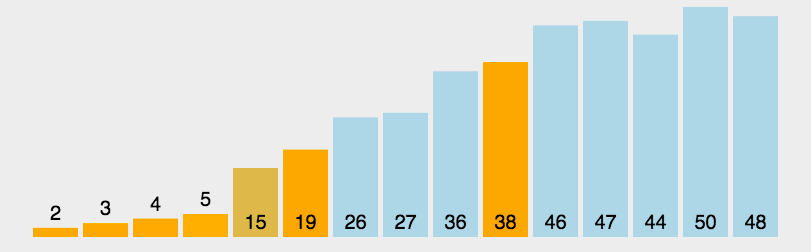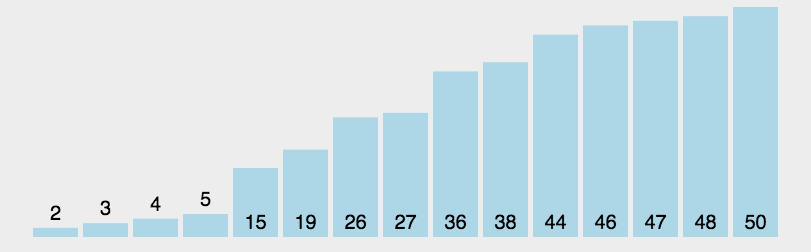
每进行一趟快速排序,都会有一个元素处于最终的位置,它左侧的元素都比他小,它右侧的元素都比他大。
1 | public static int partition(int[] arr, int left, int right) { |
这部分按照原始定义要按照下面这种写法,但是因为每次都要交换,所以改成了上面这种。因为一开始key的值已经保存了,所以不需要每次都交换。
1 | while(left<right) { |
堆排序 (heap sort)
堆:
- 大顶堆的某个节点的值总是大于等于子节点的值。
- 堆可以用数组来表示,因为堆是完全二叉树,而完全二叉树很容易存储在数组中。
- **位置k的节点的父节点的位置为$k/2$,而它的两个子节点的位置分别为$2k$和$2k+1$**,这里不使用数组索引为0的位置,是为了更清晰地描述节点的位置关系。
- 用count记录当前堆中元素个数
堆的基本操作:
在大顶堆中,当一个节点的值比父节点的值要大,那么就需要交换这两个节点。交换后还可能比它新的父节点大,因此就要不断地进行比较和交换操作。把这种操作成为**上浮(ShiftUp)**。
1
2
3
4
5
6private void shiftUp(int[] data, int k) {
while(k > 1 && data[k] > data[k/2]) {
swap(data, k, k/2);
k = k/2;
}
}类似的,当一个节点比子节点小,那么就需要不断地向下进行比较和交换操作,这种操作叫做**下沉(ShiftDown)**。一个节点如果有两个子节点,那么应该与两个子节点中最大的那个节点进行交换。
1
2
3
4
5
6
7
8
9
10
11
12private void shiftDown(int[] data, int count, int k) {
while(2*k <= count) { // 当前节点有左孩子
int j = 2*k;
if(j+1 <= count && data[j] < data[j+1])
j += 1;
//data[j] 表示左右孩子中的最大值
if(data[k] > = data[j])
break;
swap(data, k, j);
k = j;
}
}插入元素:将新元素放入数组尾部,然后执行上浮,到合适的位置
1
2
3
4
5
6private void insert(int[] data, int count, int item) {
//这个这样写是不对的,因为直接用了数组,到时候可以用list动态增加数组长度
count += 1;
data[count] = item;
shiftUp(data, count);
}删除最大元素:从大顶堆中取出堆顶元素,然后将最后一个元素移到堆顶位置,再下沉到合适的位置。
1
2
3
4
5
6private void extractMax(int[] data, int count) {
int item = data[1]; // 因为数组0位置没有存储元素
swap(data, 1, count);
shiftDown(data, 1);
count -= 1;
}
堆排序:
由于大顶堆很容易得到最大的元素并删除它,不断地进行这种操作可以得到一个递减序列。如果把最大元素和当前堆数组中的最后一个元素交换位置,并且不删除它,就可以得到一个递增序列。(其实也可以构造小顶堆,和上面的方法差不多)。堆排序是原地排序,不需要额外空间。
把MaxHeap当作一个类,上面都是他的内部函数。
1
2
3
4
5
6
7
8
9
10
11public class HeapSort {
public static void sort(int[] arr) {
int count = arr.length;
MaxHeap<Integer[]> maxHeap = new MaxHeap();
for(int i=0;i<count;i++) {
maxHeap.insert(arr, count, i);
}
for(int i=n-1;i>=0;i++)
arr[i] = maxHeap.extractMax(arr, count);
}
}
计数排序 (counting sort)
计数排序不是基于比较的排序算法,其核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。 作为一种线性时间复杂度的排序,计数排序要求输入的数据必须是有确定范围的整数。
算法描述:
- 找出待排序的数组中最大和最小的元素;
- 统计数组中每个值为i的元素出现的次数,存入数组C的第i项;
- 对所有的计数累加(从C中的第一个元素开始,每一项和前一项相加);
- 反向填充目标数组:将每个元素i放在新数组的第C(i)项,每放一个元素就将C(i)减去1。
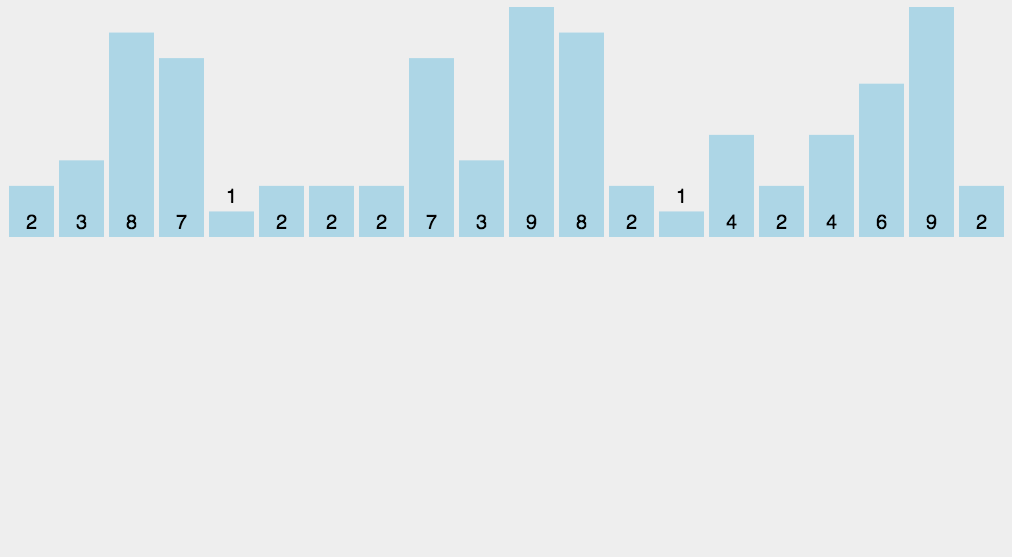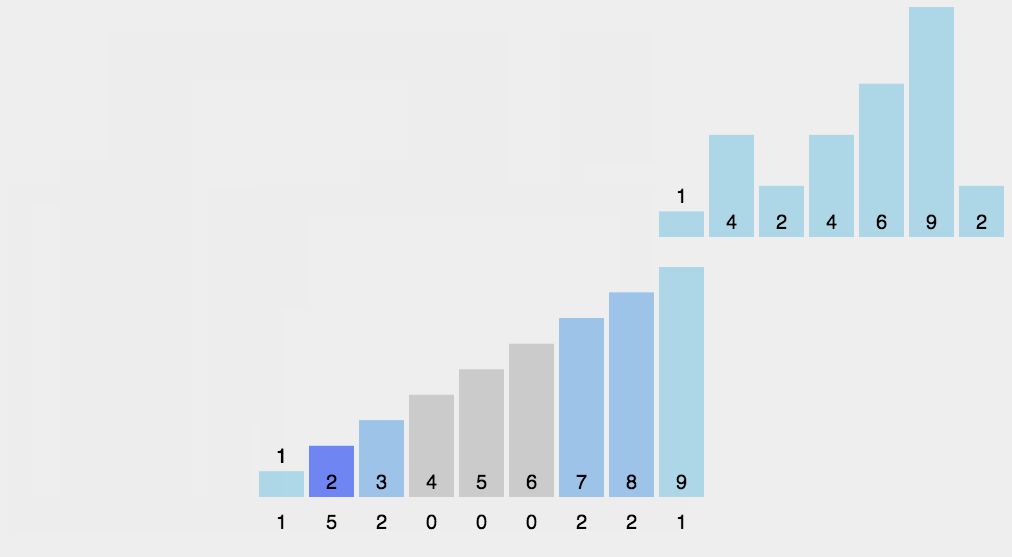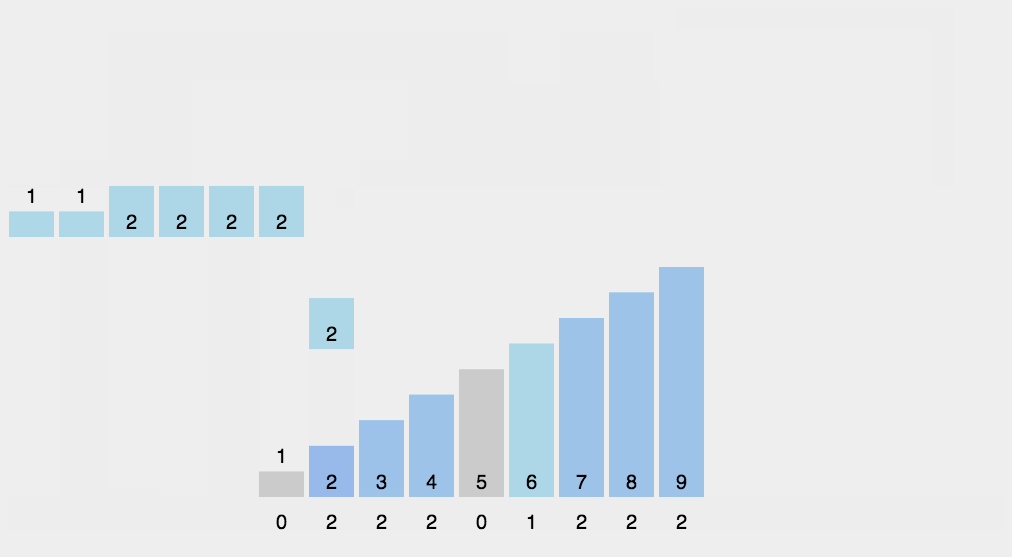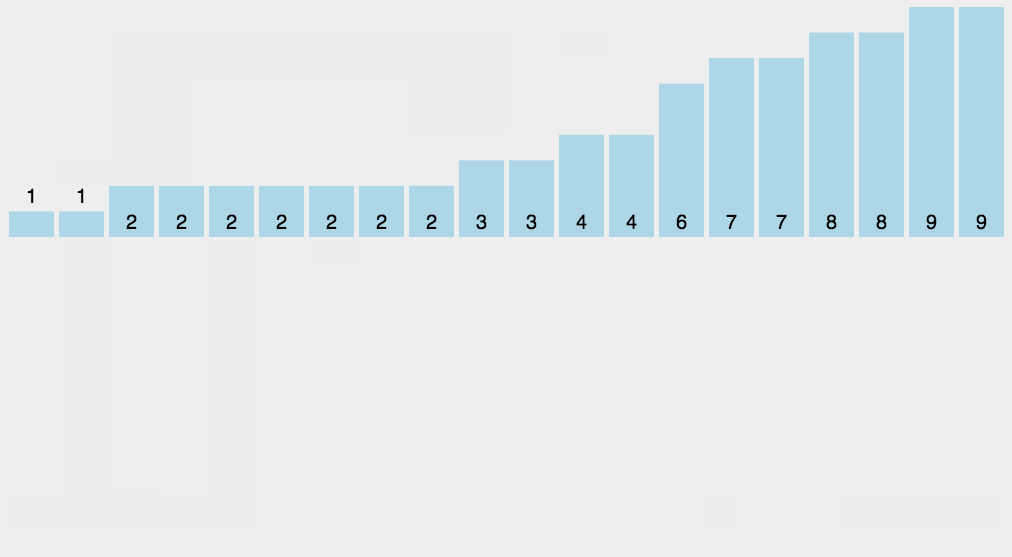
桶排序 (bucket sort)
基数排序 (radix sort)
https://www.cnblogs.com/onepixel/p/7674659.html